问题
填空题
设a,b,,c满足a+b+c=1,a2+b2+c2=2,a3+b3+c3=3则abc= .
答案
.
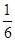题目分析：（a+b+c）2=a2+b2+c2+2（ab+bc+ac），即1=2+2（ab+bc+ac），∴ab+bc+ac=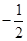
，a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-ac-bc），即3-3abc=2+
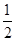，∴abc=.
搜题请搜索小程序“爱下问搜题”
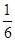设a,b,,c满足a+b+c=1,a2+b2+c2=2,a3+b3+c3=3则abc= .
.
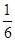题目分析：（a+b+c）2=a2+b2+c2+2（ab+bc+ac），即1=2+2（ab+bc+ac），∴ab+bc+ac=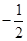，a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-ac-bc），即3-3abc=2+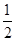，∴abc=.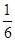