问题
问答题
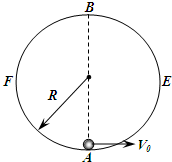
有一个竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一个质量为m的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA轨道回到点A,到达A点时对轨道的压力为4mg.
在求小球在A点的速度V0时,甲同学的解法是:由于小球恰好到达B点,故在B点小球的速度为零,
m1 2
=2mgR所以:V0=2v 20 gR
在求小球由BFA回到A点的速度时,乙同学的解法是:由于回到A点时对轨道的压力为4mg
故:4mg=m
所以:VA=2v 2A R gR
你同意甲、乙两位同学的解法吗?如果同意请说明理由;若不同意,请指出他们的错误之处,并求出结果.根据题中所描绘的物理过程,求小球由B经F回到A的过程中克服摩擦力所做的功.
答案
不同意;
甲同学在求V0时,认为小球在B点的速度为零,这是错误的,在B点VB有最小值.
正确的解法是:mg=m
①v 2B R
-2mgR=
m1 2
-v 2B
m1 2
②v 20
联立①、②求解得:v0=5gR
乙同学在计算中漏掉了重力,应为:FN-mg=m
③v 2A R
将FN=4mg代入解得:vA=3gR
设摩擦力做得功为Wf,小球从B→F→A的过程中由动能定理可得:2mgR+Wf=
m1 2
-v 2A
m1 2
④v 2B
解得:Wf=-mgR
故小球从B→F→A的过程中克服摩擦力做得功为Wf=mgR.
答:小球由B经F回到A的过程中克服摩擦力所做的功mgR.
