用长为L的细线拉一质量为m的小球,小球带电量为+q,细线一端悬于固定点O,整个装置放在水平向右一足够大的匀强电场中,小球静止时细线与竖直方向的夹角为θ,电场范围足够大,不计空气阻力,重力加速度为g,求:
(1)匀强电场的电场强度大小;
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中的最大速度大小;
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是多大?

(1)小球静止A点时,受力如图所示
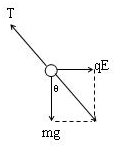
据三力平衡条件,得
tanθ=qE mg
解得,E=
①mgtanθ q
(2)小球运动到平衡位置时速度最大,由动能定理,得
qELsinθ-mgL(1-cosθ)=
mv2 ②1 2
将①式代入,得
v=
③2gL(1-cosθ) cosθ
小球从最底点到最高点时,速度为零,向心力为零,细线与竖直方向成α角,由动能定理,得
qELsinα-mgL(1-cosα)=0 ④
将①式代入④式,得
tanθsinα=1-cosα
解得,α=2θ
在最高点,重力与电场力合力的法线分力与拉力平衡,设线的拉力为F
F=mgcos2θ+qEsin2θ=mgcos2θ+mgtanθ•sin2θ=mg(2cos2θ-1)+mgtanθ•2sinθcosθ=mg
(3)设B点与A点对悬点O对称,即AB为圆轨迹的直径,当小球恰好能运动到B点时,就能在竖直面内恰好做完整的圆周运动
在B点,重力与电场力的合力提供向心力
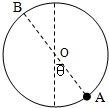
=mmg cosθ v 2B L
设将小球拉至O点正下方最低点时给它一水平向右的初速度为v0,由动能定理,得
-2mgLcosθ-qELsinθ=
mvB2-1 2
mv021 2
解得
v0=2gLcosθ+ 3gL cosθ
答:
(1)匀强电场的电场强度大小E=
;mgtanθ q
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中的最大速度大小v=
;2gL(1-cosθ) cosθ
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小为mg;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是v0=
.2gLcosθ+ 3gL cosθ
