问题
解答题
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0.
答案
证明略
证明(必要性)
∵a+b=1,∴a+b-1=0, 2分
∴a3+b3+ab-a2-b2=(a+b)(a2-ab+b2)-(a2-ab+b2) 5分
=(a+b-1)(a2-ab+b2)="0. " 7分
(充分性)
∵a3+b3+ab-a2-b2=0,
即(a+b-1)(a2-ab+b2)=0, 9分
又ab≠0,∴a≠0且b≠0,
∴a2-ab+b2=(a-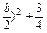 b2>0,
b2>0,
∴a+b-1=0,即a+b="1, " 12分
综上可知,当ab≠0时,a+b=1的充要条件是
a3+b3+ab-a2-b2="0. " 14分
