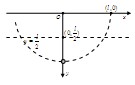
质量为m的小球悬挂于O点,悬线长为l,如图建立平面直角坐标系xOy,y轴沿悬线竖直向下。现将小球拉到(l,0)点后无初速释放,不计空气阻力和钉子的直径,试计算:
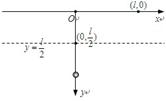
(1)如果在(0,l)点钉一枚钉子可以挡住细线,那么细线刚碰到钉子后对小球的拉力是多大?
(2)如果将钉子钉在y=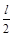 的水平虚线上某位置,要求细线碰到钉子后能够绕钉子做圆周运动通过最高点,那么钉子所钉的位置的横坐标x应该满足什么条件?
的水平虚线上某位置,要求细线碰到钉子后能够绕钉子做圆周运动通过最高点,那么钉子所钉的位置的横坐标x应该满足什么条件?
(1)F=5mg(2) <x≤
<x≤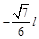 或
或  ≤x<
≤x<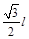
题目分析:(1)(4分)设摆到竖直时速度大小为v,悬线刚碰钉子后对小球的拉力大小为F,则由机械能守恒定律知mgh=½mv2 r=l/2 ,
由向心力公式得 F- mg = mv2/r , 联解得 F=5mg
(2)(9分)设小球恰能通过最高点时绕钉子转动的半径为r′,在最高点的速度大小为v′,
则由向心力公式得 mg = mv′ 2 /r′ (1分) 机械能守恒 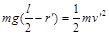 (2分),
(2分),
联解得 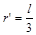 (2分)
(2分)
设这种情况下钉子的横坐标为x1,则 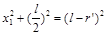 联解得
联解得 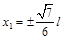
由于钉子必定在以O为圆心半径为l的圆内,设直线y=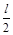 与该圆的交点横坐标为x2,
与该圆的交点横坐标为x2,
则有 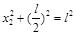 ,解得
,解得 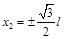
所以要让小球能通过最高点做圆周运动,钉子在直线y=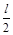 上,其横坐标必须满足
上,其横坐标必须满足
 <x≤
<x≤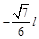 或
或  ≤x<
≤x<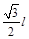 (共4分)
(共4分)
若未考虑式限制结果写成“x≤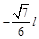 或
或  ≤x 11”也算对,即写出11也得4分。
≤x 11”也算对,即写出11也得4分。
点评:在分析圆周运动时,一定要弄清楚向心力的来源,以及运动半径的变化
