问题
问答题
在△ABC中，角A，B，C的对边分别为a，b，c，已知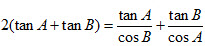
。
（Ⅰ）证明：a+b=2c；
（Ⅱ）求cosC的最小值。
答案
参考答案：
解析：（Ⅰ）由题意知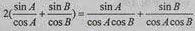
， 化简得
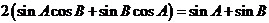， 即2sin（A+B）=sinA+sinB。
因为A+B+C=π，所以sin（A+B）=sin（π-C）=sinC。
从而sinA+sinB=2sinC。
由正弦定理得a+b=2c。
（Ⅱ）由（Ⅰ）知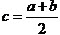
，所以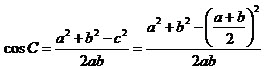
，
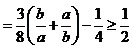当且仅当a=b时，等号成立。
故cosC的最小值为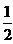
。