问题
问答题
探险队员在探险时遇到一山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状．此队员从山沟的竖直一侧，以速度v0沿水平方向跳向另一侧坡面．如图所示以沟底的O点为原点建立坐标系Oxy．已知，山沟竖直一侧的高度为2h，坡面的抛物线方程为y=
x2，探险队员的质量为m．人视为质点，忽略空气阻力，重力加速度为g．求：人落到坡面时的动能．1 2h
答案
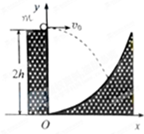
设探险队员跳到坡面上时水平位移为x，竖直位移为H，
由平抛运动规律有：x=v0t，H=
gt21 2
整个过程中，由动能定理可得：mgH=EK-
mv02．1 2
由几何关系，y=2h-H
坡面的抛物线方程y=
x2 1 2h
| 1 |
| 2 |
| 2mg2h2 |
| v02+gh |
答：人落到坡面时的动能Ek=
mv02+1 2
．2mg2h2 v02+gh