问题
问答题
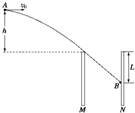
如图,两块平行金属板M、N竖直放置,两板间的电势差U=1.5×103 V,现将一质量m=1×10-2 kg、电荷量q=4×10-5 C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h=0.2m,(不计空气阻力,g=10m/s2),求:
(1)小球到达M板上端时的速度大小vM和与水平方向夹角的正切值
(2)M、N两板间的距离d,落点B距N板上端的距离L
(3)小球到达B点时的动能Ek.
答案
(1)小球做平抛运动,竖直方向上:
vy2=2gh
解得:vy=2 m/s
则小球的速度:vm=
=2v02+vy2
m/s 5
方向与水平夹角θ,tanθ=
=vy v0 1 2
(2)进入电场后做直线运动,由受力分析与几何知识得:
tanθ=
=mg F电 L d
F电=q
=2mg U d
解得:d=0.3 m,L=0.15m
(3)从A到B的过程中,应用动能定理:
mg(h+L)+qU=Ek-
mv02 1 2
解得:Ek=0.175 J
答:(1)小球到达M板上端时的速度大小为2
m/s,与水平方向夹角的正切值为5
;1 2
(2)M、N两板间的距离d为0.3m,落点B距N板上端的距离L为0.15m;
(3)小球到达B点时的动能Ek为0.175J
