问题
填空题
一条弦把圆分成2:3两部分,那么这条弦所对的圆周角的度数为_______
答案
72°或108°
先求出这条弦所对圆心角的度数,然后分情况讨论这条弦所对圆周角的度数.
解:如图,连接OA、OB.

弦AB将⊙O分为2:3两部分,
则∠AOB=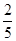 ×360°=144°;
×360°=144°;
∴∠ACB=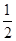 ∠AOB=72°,
∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.
一条弦把圆分成2:3两部分,那么这条弦所对的圆周角的度数为_______
72°或108°
先求出这条弦所对圆心角的度数,然后分情况讨论这条弦所对圆周角的度数.
解:如图,连接OA、OB.

弦AB将⊙O分为2:3两部分,
则∠AOB=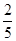 ×360°=144°;
×360°=144°;
∴∠ACB=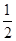 ∠AOB=72°,
∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.