解：(1)当n=10时，集合A={1，2，3，…，19，20}，

B={x∈A|x＞9}={10，11，12，…，19，20}不具有性质P．

因为对任意不大于10的正整数m，都可以找到该集合中两个元素b₁=10与b₂=10+m，使得|b₁-b₂|=m成立。

集合C={x∈A|x=3k-1，k∈N*}具有性质P．

因为可取m=1＜10，对于该集合中任意一对元素c₁=3k₁-1，c₂=3k₂-1，k₁，k₂∈N*，

都有|c₁-c₂|=3|k₁-k₂|≠1。

(2)当n=1000时，则A={1，2，3，…，1999，2 000}，

①若集合S具有性质P，那么集合T={2001-x|x∈S}一定具有性质P．

首先因为T={2 001-x|x∈S}，任取t=2001-x₀∈T，其中x₀∈S，

因为SA，所以x₀∈{1，2，3，…，2 000}，

从而1≤2 001-x₀≤2000，即t∈A，所以T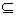A．

由S具有性质P，可知存在不大于1000的正整数m，

使得对S中的任意一对元素s₁，s₂，都有|s₁-s₂|≠m，

对于上述正整数m，从集合T={2001-x|x∈S}中任取一对元素t₁=2001-x₁，t₂=2001-x₂，其中x₁，x₂∈S， 则有|t₁-t₂|=|x₁-x₂|≠m，所以集合T= {200-x|x∈S}具有性质P。

②设集合S有k个元素，由第①问知，若集合S具有性质P，那么集合T={2001-x|x∈S} 一定具有性质P．

任给x∈S，1≤x≤2 000，则x与2001-x中必有一个不超过1 000，

所以集合S与T中必有一个集合中至少存在一半元素不超过1 000，

不妨设S中有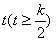个元素b₁，b₂，…，b_t不超过1 000，

由集合S具有性质P，可知存在正整数m≤1000，使得对S中任意两个元素s₁，s₂，都有|s₁-s₂|≠m，

所以一定有b₁+m，b₂+m，…，b_t+m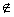S，

又b_i+m≤1 000 +1 000=2 000，故b₁+m，b₂+m，…，b_t+m∈A，

即集合A中至少有t个元素不在子集S中，

因此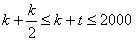，所以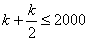，得k≤1 333，

当S={1，2，…，665 ，666，1 334，…，1 999，2 000}时，

取m=667，则易知对集合S中任意两个元素y₁，y₂，都有|y₁-y₂|≠667，即集合S具有性质P，

而此时集合S中有1 333个元素，

因此集合S的元素个数的最大值是1 333。