问题
填空题
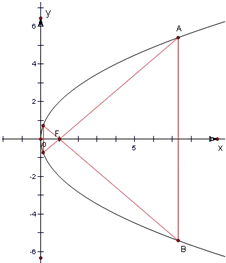
已知F是抛物线y2=4x的焦点,A,B是抛物线上两点,△AFB是正三角形,则该正三角形的边长为______.
答案
y2=4x的焦点F(1,0)
等边三角形的一个顶点位于抛物线y2=4x的焦点,另外两个顶点在抛物线上,
则等边三角形关于x轴对称,两个边的斜率k=±tan30°=±
,其方程为:y=±3 3
(x-1),3 3
与抛物线y2=4x联立,可得
(x-1)2=4x1 3
∴x=7±4
,3
当x=7+4
时,y=±2(2+3
),∴等边三角形的边长为8+43
;3
当x=7-4
时,y=±2(2-3
),∴等边三角形的边长为8-43
;3
故答案为:8±4
;3