问题
解答题
已知三个向量a ,b ,c 不共面,并且p=a+b-c ,q=2a-3b-5c ,r=-7a+18b+22c ,向量p ,q ,r 是否共面?
答案
解:实数λ,μ,使p= λq+ μr ,
则a+b-c=(2λ-7μ)a+(-3λ+18μ)b+(-5λ+22μ)c
∵a,b,c不共面,
∴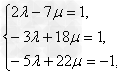
∴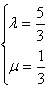
即存在实数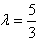 ,
,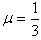 ,使p=λq+μr,故向量p、q、r共面.
,使p=λq+μr,故向量p、q、r共面.
已知三个向量a ,b ,c 不共面,并且p=a+b-c ,q=2a-3b-5c ,r=-7a+18b+22c ,向量p ,q ,r 是否共面?
解:实数λ,μ,使p= λq+ μr ,
则a+b-c=(2λ-7μ)a+(-3λ+18μ)b+(-5λ+22μ)c
∵a,b,c不共面,
∴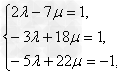
∴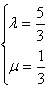
即存在实数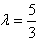 ,
,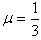 ,使p=λq+μr,故向量p、q、r共面.
,使p=λq+μr,故向量p、q、r共面.