问题
填空题
已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则y=f(x)的值域为______.
答案
[1,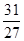 ]
]
∵f(x)=ax2+bx+3a+b是偶函数,
∴其定义域[a-1,2a]关于原点对称,
∴即a-1=-2a,∴a=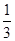 ,
,
∵f(x)=ax2+bx+3a+b是偶函数,
即f(-x)=f(x),∴b=0,
∴f(x)=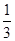 x2+1,x∈[-
x2+1,x∈[-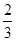 ,
,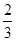 ],其值域为{y|1≤y≤
],其值域为{y|1≤y≤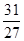 }.
}.
已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则y=f(x)的值域为______.
[1,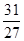 ]
]
∵f(x)=ax2+bx+3a+b是偶函数,
∴其定义域[a-1,2a]关于原点对称,
∴即a-1=-2a,∴a=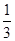 ,
,
∵f(x)=ax2+bx+3a+b是偶函数,
即f(-x)=f(x),∴b=0,
∴f(x)=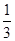 x2+1,x∈[-
x2+1,x∈[-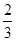 ,
,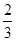 ],其值域为{y|1≤y≤
],其值域为{y|1≤y≤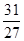 }.
}.