问题
解答题
关于复数z的方程z2-(a+i)z-(i+2)=0(a∈R),证明对任意的实数a,原方程不可能有纯虚根.
答案
见解析
证明:假设原方程有纯虚根,令z=ni,n≠0,则有(ni)2-(a+i)ni-(i+2)=0,
整理可得-n2+n-2+(-an-1)i=0,
所以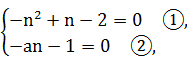
则对于①,判别式Δ<0,方程①无解,故方程组无解,故假设不成立,
所以原方程不可能有纯虚根.
关于复数z的方程z2-(a+i)z-(i+2)=0(a∈R),证明对任意的实数a,原方程不可能有纯虚根.
见解析
证明:假设原方程有纯虚根,令z=ni,n≠0,则有(ni)2-(a+i)ni-(i+2)=0,
整理可得-n2+n-2+(-an-1)i=0,
所以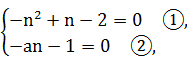
则对于①,判别式Δ<0,方程①无解,故方程组无解,故假设不成立,
所以原方程不可能有纯虚根.