问题
填空题
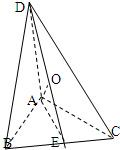
在平面几何里有射影定理:设△ABC的两边AB⊥AC,D是A点在BC边上的射影,则AB2=BD•BC.拓展到空间,在四面体A-BCD中,DA⊥面ABC,点O是A在面BCD内的射影,且O在△BCD内,类比平面三角形射影定理,△ABC,△BOC,△BDC三者面积之间关系为______.
答案
由已知在平面几何中,
若△ABC中,AB⊥AC,AE⊥BC,E是垂足,
则AB2=BD•BC,
我们可以类比这一性质,推理出:
若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,
则(S△ABC)2=S△BOC.S△BDC.
故答案为:(S△ABC)2=S△BOC.S△BDC