如图所示,质量为m=1kg的小滑块,从光滑、固定的 圆弧轨道的最高点A由静止滑下,经最低点B后滑到位于水平面的木板上.已知木板质量M=2kg,其上表面与圆弧轨道相切于B点,且长度足够长.整个过程中木板的
圆弧轨道的最高点A由静止滑下,经最低点B后滑到位于水平面的木板上.已知木板质量M=2kg,其上表面与圆弧轨道相切于B点,且长度足够长.整个过程中木板的 图像如图所示,g=l0m/s2.
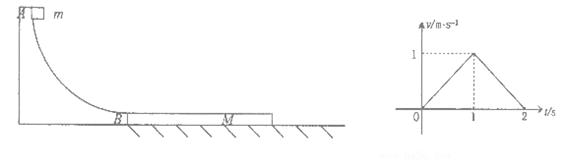
图像如图所示,g=l0m/s2.
求:(1)滑块经过B点时对圆弧轨道的压力.
(2)滑块与木板之间的动摩擦因数.
(3)滑块在木板上滑过的距离.
(1)30 N,竖直向下(2)0.5 (3)3m.
题目分析:(1)滑块下滑过程,由机械能守恒定律得 mgR= mv2
mv2
由向心力公式得N′-mg=m
解得N′=mg+m ="30" N
="30" N
根据牛顿第三定律,滑块对轨道的压力是30 N,方向竖直向下.
(2)由v-t图象得:木板的加速度是a1=1m/s2
滑块与木板共同减速的加速度大小a2=1m/s2
设木板与地面间的动摩擦因数是μ1
滑块与木板之间的动摩擦因数是μ2
在1-2s内,对滑块和木板:μ1(M+m)g=(M+m)a2
在0-1s内,对木板:μ2mg-μ1(M+m)g=Ma1
解得:μ1=0.1,μ2=0.5
(3)滑块在木板上滑动的过程中,v1是它们的共同速度,t1是它们达到共同速度所用的时间
对滑块:μ2mg=ma v1=v-at1 木板的位移x1=
滑块的位移x2=
滑块在木板上滑动的距离△x=x2-x1=3m
