①当两三角形一个顶角为40°，另一个底角为40°，此时40°角为内角的两个等腰三角形不相似；故此选项错误；

②反比例函数y=-

2

x

，当x＞0时，y随x的增大而增大；故此选项错误；

③两圆的半径分别是3和4，圆心距为d，若两圆有公共点，1≤d≤7，故此选项错误；

④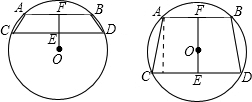利用垂径定理和勾股定理可知：OE=3，OF=4，

a．如图，∵4-3=1，（8-6）÷2=1，

∴AC=

2

；

b．如图，∵4+3=7，（8-6）÷2=1，

∴AC=5

2

．

c．如右图，连接AO，OC，由r=5，AB=6，CD=8，

可得OE=4，OF=3，EF=7，

∵AB∥CD，∴△EGC∽△AGF

∴

EG

GF

=

EC

AF

=

3

4

，

∴

4-OG

3+OG

=

3

4

，

∴OG=1，

∴EG=4-1=3，OF=3+1=4，

∴CG=3

2

，

AG═4

2

，

AC=AG+CG=3

2

+4

2

=7

2

．

因此，弦AC的长为

2

或5

2

或7

2

．故此选项错误．

⑤函数y=-（x-3）²+4（-1≤x≤4）的最大值是4，最小值是当x=-1时y=-12，故此选项错误．

故全部错误，

故选：A．