问题
解答题
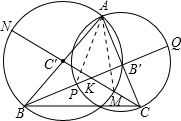
给出锐角△ABC,以AB为直径的圆与AB边的高CC′及其延长线交于M,N.以AC为直径的圆与AC边的高BB′及其延长线将于P,Q.求证:M,N,P,Q四点共圆.
(第19届美国数学奥林匹克)
答案
证明:设PQ,MN交于K点,连接AP,AM.
由射影定理,得AM*AM=AC'*AB,AP*AP=AC*AB',又B、C、B'、C'四点共圆,
由切割线定理,AC'*AB=AC*AB',
∴AM=AP,又AM=AN,AP=AQ(垂直于直径的弦性质),
∴AM=AP=AN=AQ,M、N、P、Q是共圆心为A的圆.
须证MK•KN=PK•KQ,
即证(MC′-KC′)(MC′+KC′)
=(PB′-KB′)•(PB′+KB′)
或MC′2-KC′2=PB′2-KB′2.①
∵AP=AM(所对弧长相等),
从而有AB′2+PB′2=AC′2+MC′2.
故MC′2-PB′2=AB′2-AC′2
=(AK2-KB′2)-(AK2-KC′2)
=KC′2-KB′2.②
由②即得①,命题得证.