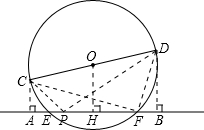
已知直线l与⊙O交于不同的两点E,F,CD是⊙O的直径,CA⊥l,DB⊥l,垂足分别为A,B.若AB=7,BD-AC=1,AE=1,试问在线段AB上是否存在点P,使得以点P,A,C为顶点的三角形与以点P,B,D为顶点的三角形相似?若存在,求出AP的长;若不存在,请说明理由.
(1)若l与直径CD不相交,如图所示,
(i)作OH⊥AB于H,易得AE=BF,此时△ACE∽△BED,△AFC∽△BDF,
则E,F为满足的点,故AP=AE=1或AP=AF=AB-BF=6
(ii)若除E,F外还存在点P使△APC∽△BPD,设AC=x,BD=y,则y-x=1,
∵Rt△ACE∽Rt△BED,故=,得xy=6
于是x=2,y=3或x=-3,y=-2(舍去)
∵△APC∽△BPD,故=,即=,解得AP=,
故存在第三个满足条件的点P,且AP=.
综合(i),(ii),满足条件的点有三个,AP的长分别为1,6,.
(2)若l与直径CD相交,且交点为Q,如图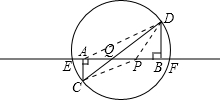
(i)由∠AQC=∠DQB,得Rt△ACQ∽Rt△BDQ,则点Q为满足条件的点,
设AC=x,BD=y,则y-x=1,
又∠DEB=∠ECA,则Rt△ACE∽Rt△BED,
故=,得xy=8,
于是,x=,y=或x=,y=(舍去)
∵Rt△ACQ∽Rt△BDQ,∴=,解得AQ=.
(ii)若除Q外,还存在点P,使△APC∽△BDP,则=,
整理得AP2-7AP+8=0,解得AP=.
综合(i),(ii),满足条件的点P有三个,AP的长分别为,,.
所以,综合(1)(2)可得,满足条件的点共有6个.AP的长度为:
1,6,,,,.