问题
填空题
正六边形的面积是18
|
答案
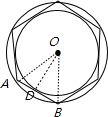
如图所示,设正多边形的边长为a,
∵正六边形的面积是18
,3
∴△OAB的面积是3
,即3
AB•OA•sin60°=31 2
,3
a2•1 2
=33 2
,3
∴a=2
,3
∴OD=OA•sin60°=2
•3
=3,3 2
∴S圆环=S外接圆-S内切圆=π•(2
)2-π•32=12π-9π=3π.3
故答案为:3π.
正六边形的面积是18
|
如图所示,设正多边形的边长为a,
∵正六边形的面积是18
,3
∴△OAB的面积是3
,即3
AB•OA•sin60°=31 2
,3
a2•1 2
=33 2
,3
∴a=2
,3
∴OD=OA•sin60°=2
•3
=3,3 2
∴S圆环=S外接圆-S内切圆=π•(2
)2-π•32=12π-9π=3π.3
故答案为:3π.
