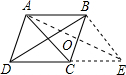
问题
填空题
在梯形ABCD中,AB∥DC,AB=AC=AD=
|
答案
如图,过B作BE∥AC交CD的延长线于E,
∵AB∥CE
∴四边形ACEB是平行四边形,而AB=AC,
∴四边形ABEC是菱形
∴BE=AC=AD
∴四边形ABED是等腰梯形
∴AE=BD,设AE于BC交于O,根据菱形的性质得:∠COE=90°,OC=
BC=1 2 2 2
CE=AB=
,3
∴OE=
=
2-(3
)22 2
,10 2
∴AE=2OE=
,10
∴BD=
.10