问题
填空题
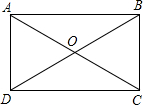
矩形的周长是16,两对角线夹角为60°,则矩形较长的对角线的长度是______.
答案
如下图所示:∠AOD=60°,
∵四边形ABCD是矩形
∴OA=OD=OB=OC(矩形的对角线相等且互相平分)
又∵∠AOD=60°
∴OA=OD=AD,∠DAO=60°
在Rt△ADC中,tan∠DAO=
=tan60°=DC AD
,3
即:DC=
AD,3
又∵AB+AD+DC+BC=16,即:AD+DC=
×16=8=(1 2
+1)AD3
∴AD=
=4(8
+13
-1),3
∴AC=
=4(AD cos∠AOD
-1)×3
=81 cos60°
-8,3
所以,矩形较长的对角线的长度是:8
-8.3