问题
解答题
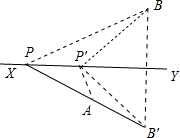
在定直线XY异侧有两点A、B,在直线XY上求作一点P,使PA与PB之差的绝对值最大.
答案
作法:作点B关于直线XY的对称点B′,
作直线AB′交XY于P点,
则点P为所求点(如图)若B′A∥XY(即B′、A到直线XY的距离相等),
则点P不存在.
证明:连接BP,在XY上任意取点P′,
连接P′A、P′B,则PB=PB′,P′B=P′B,
因为|P′B-P′A|=|PB′-P′A|<AB′=|P′B-PA|=|PB-PA|,
所以,此时点P使|PA-PB|最大.