问题
解答题
写出一个用二分法求方程2x=x3的近似解(精确到0.0001)的算法。
答案
解:令f(x)=x3-2x,
∵f(1)<0,f(2)>0,
∴f(x)在(1,2)上必有零点
S1,令x1=1,x2=2,f(x)=x3-2x
S2,计算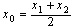
S3,计算f(x0),判断f(x0)是否为0,若f(x0)=0,则输出“x0是方程的解”,否则执行S4
S4,若f(x0)<0,则令x1=x0,否则令x2=x0
S5,判断|x1-x2|<0.0001是否成立,若成立,则输出“x0是方程的解”否则转到S2继续执行。
