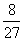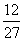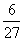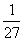问题
解答题
“石头、剪刀、布”是一种广泛流传于我国民间的古老游戏,其规则是:用三种不同的手势分别表示石头、剪刀、布;两个玩家同时出示各自手势1次记为1次游戏,“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”;双方出示的手势相同时,不分胜负。现假设玩家甲、乙双方在游戏时出示三种手势是等可能的.
(Ⅰ)求出在1次游戏中玩家甲胜玩家乙的概率;
(Ⅱ)若玩家甲、乙双方共进行了3次游戏,其中玩家甲胜玩家乙的次数记作随机变量X,求X的分布列及其期望.
答案
解:(1)玩家甲、乙双方在1次游戏中出示手势的所有可能结果是:(石头,石头);(石头,剪刀);(石头,布);(剪刀,石头);(剪刀,剪刀);(剪刀,布);(布,石头);(布,剪刀);(布,布),共有9个基本事件,
玩家甲胜玩家乙的基本事件分别是:(石头,剪刀);(剪刀,布);(布,石头),共有3个,
所以,在1次游戏中玩家甲胜玩家乙的概率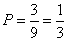 。
。
(2)X的可能取值分别为0,1,2,3,
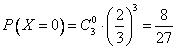 ,
,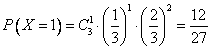 ,
,
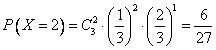 ,
,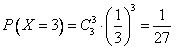 ,
,
X的分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
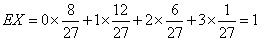 。
。