解：第一步，令f(x)=x²-2,给定精确度d.

第二步，确定区间［a,b］，满足f(a)·f(b)＜0.

第三步，取区间中点m=.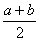

第四步，若f(a)·f(m)＜0，则含零点的区间为［a,m］；否则，含零点的区间为［m,b］.将新得到的含零点的区间仍记为［a,b］.

第五步，判断［a,b］的长度是否小于d或f(m）是否等于0.若是，则m是方程的近似解；否则，返回第三步.

当d=0.005时，按照以上算法，可以得到下表.

a	b	|a-b|
1	2	1
1	1.5	0.5
1.25	1.5	0.25
1.375	1.5	0.125
1.375	1.437 5	0.062 5
1.406 25	1.437 5	0.031 25
1.406 25	1.421 875	0.015 625
1.414 062 5	1.421 875	0.007 812 5
1.414 062 5	1.417 968 75	0.003 906 25

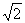   于是，开区间（1.414 062 5,1.417 968 75）中的实数都是当精确度为0.005时的原方程的近似解.实际上，上述步骤也是求的近似值的一个算法.

分析：令f(x)=x²-2,则方程x²-2="0" (x＞0)的解就是函数f(x)的零点.

“二分法”的基本思想是：把函数f(x)的零点所在的区间［a,b］(满足f(a)·f(b)＜0）“一分为二”，得到［a,m］和［m,b］.根据“f(a)·f(m)＜0”是否成立，取出零点所在的区间［a,m］或［m,b］，仍记为［a,b］.对所得的区间［a,b］重复上述步骤，直到包含零点的区间［a,b］“足够小”，则［a,b］内的数可以作为方程的近似解.