问题
解答题
用二分法设计一个求方程x2-2=0的正近似根的算法(设所求近似根与精确解的差的绝对值不超过0.005).
答案
解：S1 令f(x)=x2-2，因为f(1)＜0，f(2)＞0，所以设x1=1，x2=2.
S2 令m=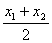
，判断f(m)是否为0.若是，则m为所求；若否，则继续判断f(x1)·f(m)大于0还是小于0.
S3 若f(x1)·f(m)＞0，则令x1=m；否则，令x2=m.
S4 判断|x1-x2|＜0.005是否成立,若是，则x1、x2之间的任意值均为满足条件的近似根；若否，则返回第二步.
该算法实质是求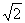
的近似值的一个最基本的方法.