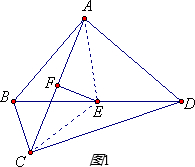
（1）如图，EF垂直平分AC．理由如下：

连接AE、CE，

∵∠A=∠C=90°，

点E、F分别是对角线AC、BD的中点，

∴AE=CE=

1

2

BD，

∴EF垂直平分AC．

（2）∵EF=

1

4

BD，AE=CE=

1

2

BD，

∴EF=

1

2

AE．

∵EF⊥AC，∠ECA=∠EAC=30°，

∴∠AEC=180°-∠ECA-∠EAC=120°，

∵AE=DE=

1

2

BD，

∴∠AEB=∠ADE+∠DAE，=2∠ADE，

∴∠ADE=

1

2

∠AEB，

同理∠CDE=

1

2

∠CEB，

如图1，∠ADC=

1

2

∠AEB+

1

2

∠CEB=

1

2

∠AEC=60°；

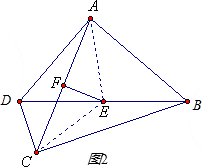
如图2，∠ADC=

1

2

∠AEB+

1

2

∠CEB=

1

2

(360°-∠AEC)=120°．

答：∠ADC的大小是60°或120°．