问题
解答题
某娱乐中心拟举行“春节”庆祝活动,每位来宾交30元入场费,可参加一次抽奖活动,抽奖活动规则是:从一个装有分值分别为1,2,3,4,5,6六个相同小球的抽奖箱中,有放回地抽取两次,每次抽取一个球,规定:若抽得两球分值之和为12分,则获得价值为m元礼品;若抽得两球分值之和为11分或10分,则获得价值为100元礼品;若抽得两球分值之和小于10分,则不获奖。
(1)求每位会员获奖的概率;
(2)假设这次活动中,娱乐中心既不赔钱,也不嫌钱,则m应为多少元?
答案
解:(1 )设每位会员获奖的事件为A,
则事件A表示抽得两球分值之和为12分或抽得两球分值之和为11分或10分,
由已知,从一个装有分值分别为1,2,3,4,5,6六个相同小球抽奖箱中,有放回地抽取两次,所得所有结果数(列表略)共有:36个,
易知,其中的事件A共有6个,
所以P(A)=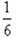 。
。
(2)设每位来宾抽奖后,娱乐中心获利为随机变量ξ元,
则ξ可能取值为三种30-m,-70,30,
而其中每种可能情况下相应的概率分别为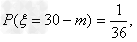
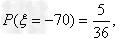
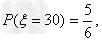
则随机变量ξ的分布列为:
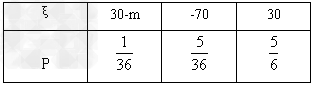 ,
,
从而求得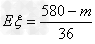 ,
,
若这次活动中娱乐中心既不赔钱也不赚钱,则Eξ=0,
所以m=580元。
