问题
解答题
为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛．该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序．通过预赛，选拔出甲、乙等五支队伍参加决赛．
（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；
（Ⅱ）若决赛中甲队和乙队之间间隔的队伍数记为X，求X的分布列和数学期望．
答案
解：（Ⅰ）设“甲、乙两支队伍恰好排在前两位”为事件A，
则P（A）=
=
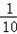
所以 甲、乙两支队伍恰好排在前两位的概率为
．
（Ⅱ）随机变量X的可能取值为0，1，2，3
P（X=0）=
=
；
P（X=1）=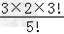
=
；
P（X=2）=
=
；
P（X=3）=
=
所以X的分布列为
∴EX=0×
+1×
+2×
+3×
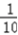=1
