问题
解答题
（选做题）
某城市有甲、乙、丙、丁4个旅游景点，一位客人游览这4个景点的概率都是0.6，且客人是否游览哪个景点互不影响．设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．
（Ⅰ）求ξ的分布列及数学期望；
（Ⅱ） 记“函数f（x）=x2﹣3ξx+1在区间[4，+∞）上单调递增”为事件A，求事件A的概率．
答案
解：（1）分别设“客人游览甲景点”、“客人游览乙景点”、“客人游览丙景点”、 “客人游览丁景点”为事件A1，A2，A3，A4，
由已知A1，A2，A3，A4相互独立，且
P（A1）=P（A2）=P（A3）=P（A4）=0.6．
客人游览的景点数的可能取值为0，1，2，3，4；
相应的，客人没有游览的景点数的可能取值为4，3，2，1，0．
所以ξ的可能取值为0，2，4．
，
，
。
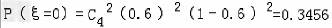所以ξ的分布列为
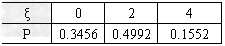
E=0×0.3452+2×0.4992+4×0.1552=1.6192．
（2）因为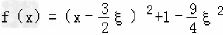
，
所以函数f（x）=x2﹣3ξx+1在区间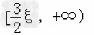
上单调递增．
要使f（x）在[4，+∞）上单调递增，当且仅当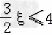
，即
．
从而
．
