问题
解答题
质地均匀的正四面体玩具的4个面上分别刻着数字1,2,3,4,将4个这样的玩具同时抛掷于桌面上.
(1)求与桌面接触的4个面上的4个数的乘积不能被4整除的概率;
(2)设ξ为与桌面接触的4个面上数字中偶数的个数,求ξ的分歧布列及期望Eξ.
答案
(1)不能被4整除的有两种情形;
①4个数均为奇数,概率为P1=(
)4=1 2 1 16
②4个数中有3个奇数,另一个为2,
概率为P2=
(C 34
)3?1 2
=1 4 1 8
这两种情况是互斥的,
故所求的概率为P=
+1 16
=1 8 3 16
(2)ξ为与桌面接触的4个面上数字中偶数的个数,由题意知ξ的可能取值是0,1,2,3,4,
根据符合二项分布,得到
P(ξ=k)=
(C k4
)4(k=0,1,2,3,4),ξ的分布列为1 2
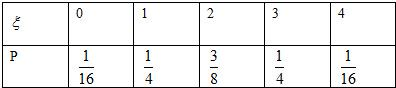
∵ξ服从二项分布B(4,
),1 2
∴Eξ=4×
=2.1 2
