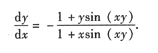参考答案：

解析：本题是一道典型的综合题，考查的知识点是隐函数；的求导计算和切线方程的求法．

[分析]： 本题的关键是由已知方程求出y’，此时的y’中通常含有x和y，因此需由原方程求出当x=0时的y值，继而得到y’的值，再写出过点(0，1)的切线方程． 计算由方程所确定的隐函数y(x)的导数；通常有三种方法：直接求导法(此时方程中的y是 x的函数)、公式法(隐函数的求导公式)和微分法(等式两边求微分)． 解法一 直接求导法．等式两边对x求导，得 -sin(xy)·(y+xy’)=1+y’ 解得

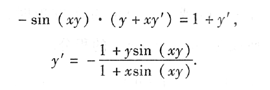解法二 公式法．设 F(x，y)=cos(xy)-x-y，

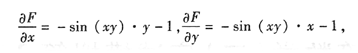所以

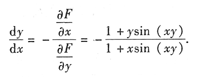解法三 微分法．等式两边求微分，得 d cos(xy)=d(x+y)，-sin(xy)(ydx+xdy)=dx+dy， -[1+x sin(xy)]dy=[1+ysin(xy)]dx， 所以