问题
解答题
今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩。现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩。
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台。
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少。
答案
解:(1)①丙种柴油发电机的数量为10-x-y;
②∵4x+3y+2(10-x-y)=32,∴y=12-2x;
(2)丙种柴油发电机为10-x-y=(x-2)台,
W=130x+120(12-2x)+100(x-2)=-10x+1240,
依题意解不等式组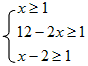 ,得:3≤x≤5.5,
,得:3≤x≤5.5,
∵x为正整数,
∴x=3,4,5,
∵W随x的增大而减少,
∴当x=5时,W最少为-10×5+1240=1190(元)。
