问题
解答题
在10件产品中,有3件一等品,4件二等品,3件三等品,从这10件产品中任取3 件,求:
(1)取出的3件产品中一等品件数X的分布列和数学期望;
(2)取出的3件产品中一等品件数多于二等品件数的概率。
答案
解:(1)由于从10件产品中任取3件的结果数为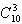
从10件产品中任取3件,其中恰有k件一等品的结果数为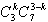
那么从10件产品中任取3件,其中恰有k件一等品的概率为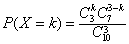 ,
,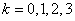
所以随机变量X的分布列是:

X的数学期望 ;
;
(2)设“取出的3件产品中一等品件数多于二等品件数”为事件A,“恰好取出1件一等品和2件三等品”为事件A1,“恰好取出2件一等品”为事件A2,“恰好取出3件一等品”为事件A3,由于事件A1,A2,A3彼此互斥,且A=A1∪A2∪A3,而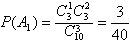 ,
,
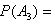
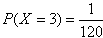
所以取出的3件产品中一等品件数多于二等品件数的概率为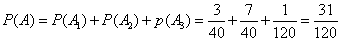 。
。
