问题
解答题
莆田四中高二年级设计了一个实验学科的能力考查方案:考生从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.规定:至少正确完成其中2道题的便可通过该学科的能力考查.已知6道备选题中考生甲能正确完成其中4道题,另2道题不能完成;考生乙正确完成每道题的概率都为
(Ⅰ)求考生甲能通过该实验学科能力考查的概率; (Ⅱ)记所抽取的3道题中,考生甲能正确完成的题数为ξ,写出ξ的概率分布,并求Eξ及Dξ; (Ⅲ)试用统计知识分析比较甲、乙考生在该实验学科上的能力水平. |
答案
(Ⅰ)∵考生甲要通过实验考查,就必须正确完成所抽三道题中的2道或3道.
∴所求概率为P=
=C 24
+C 12 C 34 C 36 4 5
(Ⅱ)由已知,ξ=0,1、2、3,
P(ξ=1)=
=C 14 C 22 C 36
,P(ξ=2)=1 5
=C 24 C 12 C 36
,P(ξ=3)=3 5
=C 34 C 36
.1 5 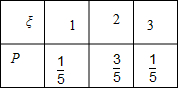
所以考生甲正确完成实验操作的题数的概率分布列为:
Eξ=1×
+2×1 5
+3×3 5
=21 5
(Ⅲ)乙考生正确完成题数η的概率分布列为:
| x2 | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
|
∴Eξ=Eη,表明甲、乙两考生正确完成题数的平均取值相同.
∵Dξ=(1-2)2×
+(2-2)2×1 5
+(3-2)2×3 5
=1 5 2 5
Dη=(0-2)2×
+(1-2)2×1 27
+(2-2)2×2 9
+(3-2)2×4 9
=8 27 2 3
∴Dξ<Dη,这表明ξ的取值比η的取值相对集中于均值2的周围,
因此甲生的实际操作能力比乙生强.
