问题
解答题
从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?
答案
解:首先,如下61个数:11,11+33,11+2×33,…,11+60×33(即1991)满足题设条件.
另一方面,设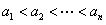 是从1,2,…,2010中取出的满足题设条件的数,对于这n个数中的任意4个数
是从1,2,…,2010中取出的满足题设条件的数,对于这n个数中的任意4个数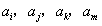 ,因为
,因为
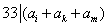 ,
,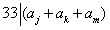
所以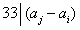 。
。
因此,所取的数中任意两数之差都是33的倍数
设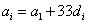 ,i=1,2,3,…,n
,i=1,2,3,…,n
由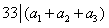 ,得
,得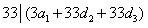
所以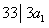 ,
,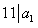 ,即
,即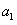 ≥11
≥11
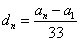 ≤
≤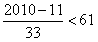
故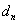 ≤60, 所以,n≤61
≤60, 所以,n≤61
综上所述,n的最大值为61。
