问题
解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
答案
(1)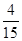 (2) X的分布列为
(2) X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 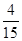 | 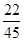 |  |  |
解:(1)设“从第一小组选出的2人均选《矩阵变换和坐标系与参数方程》”为事件A,“从第二小组选出的2人均选《矩阵变换和坐标系与参数方程》”为事件B.
由于事件A、B相互独立,
所以P(A)=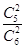 =
=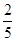 ,P(B)=
,P(B)=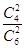 =
=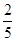 ,
,
所以选出的4人均选《矩阵变换和坐标系与参数方程》的概率为P(A·B)=P(A)·P(B)=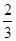 ×
×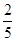 =
=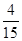 .
.
(2)X可能的取值为0,1,2,3,则
P(X=0)=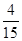 ,P(X=1)=
,P(X=1)=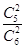 ·
·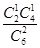 +
+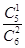 ·
·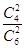 =
=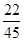 ,
,
P(X=3)=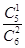 ·
·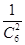 =
= .
.
P(X=2)=1-P(X=0)-P(X=1)-P(X=3)= .
.
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 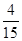 | 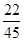 |  |  |
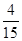 +1×
+1×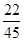 +2×
+2× +3×
+3× =1 (人).
=1 (人). 