问题
填空题
一个袋子里装有大小相同的3个红球和2个黄球,从中取出2个,含红球个数的数学期望是 .
答案
1.2
〈法一〉从5个球中取出2个球,出现红球个数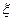 的分布列为
的分布列为
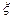 | 0 | 1 | 2 |
| P | 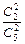 | 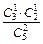 | 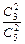 |
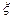 | 0 | 1 | 2 |
| P | 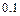 |  | 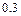 |
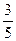
〈法二〉设取出黄球个数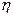 ,则
,则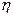 的分布列为
的分布列为
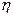 | 0 | 1 | 2 |
| P | 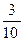 | 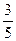 | 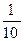 |
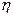 )=0×
)=0×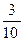 +1×
+1×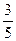 +2×
+2×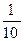 =0.8
=0.8故知红球个数的数学期望为1.2
一个袋子里装有大小相同的3个红球和2个黄球,从中取出2个,含红球个数的数学期望是 .
1.2
〈法一〉从5个球中取出2个球,出现红球个数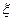 的分布列为
的分布列为
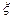 | 0 | 1 | 2 |
| P | 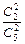 | 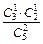 | 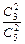 |
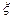 | 0 | 1 | 2 |
| P | 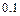 |  | 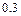 |
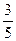
〈法二〉设取出黄球个数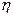 ,则
,则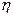 的分布列为
的分布列为
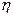 | 0 | 1 | 2 |
| P | 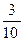 | 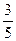 | 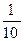 |
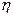 )=0×
)=0×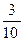 +1×
+1×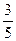 +2×
+2×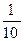 =0.8
=0.8故知红球个数的数学期望为1.2