见解析

解：设正面的次数是η，由题意η服从二项分布B(n，0.5)，

概率分布为P(η=k)=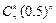，k=0，l，……，n，

且Eξ=0.5n，Dξ=0.25n；而反面次数为n－η，从而ξ=η－(n－η)=2η－n,

于是，ξ的概率分布为  P(ξ=2η－n)＝P(η="k)=" 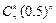， k=0，1，……，n；

即P(ξ=k)=P(η=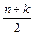)=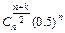，k=－n，－n+2，－n+4，……，n

故Eξ=E(2η－n)=2Eξ－n=2×0.5n－n=0；Dξ=D(2η－n)=22Dξ=4×0.25n＝n