问题
解答题
经选拔,某同学获得了参加A、B、C三所大学的自主招生考试的资格,已知某同学选择参加A大学测试而不选择B和C大学的概率为0.16,选择参加A和B大学测试而不选择C大学的概率为0.24,三所大学都不被选择的概率为0.4。假设该同学选择参加哪所大学测试互不影响。用ξ表示该同学选择的大学个数与未选大学个数之差。
(1)求ξ的分布列与数学期望;
(2)记“关于x的方程|x|-ξx=1有负根而无正根”为事件W,求事件W发生的概率P(W)。
答案
解:(1)设该同学选择参加A、B、C三所大学的自主招生考试的概率分布为P1、P2、P3,由题意得
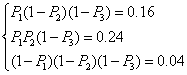
解得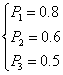
由题意知ξ的取值为3、1、-1、-3,ξ的分布列为

∴ξ的数学期望为Eξ=3×0.24 +1×0.46+(-1)×0.26+(-3)×0.04=0.8。
(2)关于x的方程|x|-ξx=1,即|x|=ξx+1,结合函数图象易知,要使该方程有根而无正根,则ξ≥1,
∴ξ=1,3,
从而P(W)=0.24+0.46=0.7。
