(本小题满分13分)
一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.
(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;
(Ⅱ)求取出的3个球中恰有2个球编号相同的概率;
(Ⅲ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.
(1)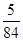 ;(2)
;(2)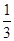 ;(3)
;(3)
第一问中利用古典概型概率公式可知,所有的基本事件数为 ,那么取出的3个球颜色相同且编号是三个连续整数的基本事件数为5,可知概率值为5/84
,那么取出的3个球颜色相同且编号是三个连续整数的基本事件数为5,可知概率值为5/84
第二问中,因为取出的3个球中恰有2个球编号相同的情况共有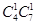 ,同上结合古典概型概率公式得到概率值
,同上结合古典概型概率公式得到概率值
第三问中,首先求解随机变量的取值,然后分别求解概率值,得到分布列和期望值。
解:(Ⅰ)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,则
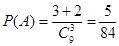 .
.
答:取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为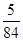 .…4分
.…4分
(Ⅱ)设“取出的3个球中恰有两个球编号相同”为事件B,则
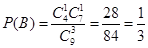 .
.
答:取出的3个球中恰有两个球编号相同的概率为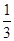 . ……8分
. ……8分
(Ⅲ)X的取值为2,3,4,5.
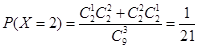 ,
,  ,
,
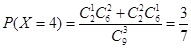 ,
, 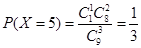 . ……11分
. ……11分
所以X的分布列为

X的数学期望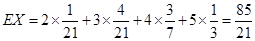 . ……13分
. ……13分
