阅读理解。
At the beginning of my 8:00 a.m. class one Monday at UNLV(拉斯维加斯内华达大学),
I cheerfully asked my students how their weekend had been. One young man said that his
weekend had not been very good. The young man then proceeded to ask me why I always
seemed to be so cheerful.
His question reminded me of something I'd read somewhere before: "Every morning when
you get up, you have a choice about how you want to approach life that day," I said to the
young man. "I choose to be cheerful."
"Let me give you an example," I continued. "In addition to teaching here at UNLV, I also
teach out at the community college in Henderson. One day a few weeks ago I drove to
Henderson. I exited the freeway and turned onto College Drive. But just then my car died.
I tried to start it again, but the engine wouldn't turn over. So I put my flashers on, grabbed
my books, and marched down the road to the college."
"As soon as I got there, the secretary in the Provost's office asked me what had happened.
'This is my lucky day', I replied, smiling."
"Your car breaks down and today is your lucky day?" She was puzzled, "What do you
mean?"
"I live seventeen miles from here. I replied. My car could have broken down anywhere
along the freeway. It didn't. Instead, it broke down in the perfect place: off the freeway, within
walking distance of here. I'm still able to teach my class, and I've been able to arrange for the
tow truck to meet me after class. If my car was meant to break down today, it couldn't have
been arranged in a more convenient fashion."
1. If you want to be cheerful you should ___________.
A. try to succeed in doing everything
B. try to please your boss every day
C. earn a lot of money by working
D. choose to be cheerful every day
2. The underlined phrase "turn over" in the third paragraph means "________"
A. roll over
B. work normally
C. stopped suddenly
D. move around
3. According to this passage we can infer that the teacher's car broke down ____.
A. near UNLV
B. along the highway
C. near Henderson
D. at the community college
4. Which one of the following is TRUE?
A. The teacher taught not only at UNLV but also at the community college.
B. That was the teacher's lucky day because the teacher liked walking.
C. The teacher always hoped that the car would break down often.
D. The young man was sad because his car broke down.
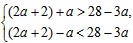 可解得
可解得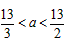
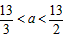 ;
;