问题
解答题
甲、乙两名射手各打了10发子弹，其中甲击中环数与次数如下表
(2)比较甲，乙两人射击水平的优劣． |
答案
(1) 0.21 p＝0.4
解：(1)由0.2＋0.3＋p＋0.1＝1，得p＝0.4.
设甲，乙两人击中的环数分别为X1，X2，则
P(X1＝8)＝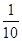
＝0.1，
P(X1＝9)＝
＝0.2，
P(X1＝10)＝
＝0.4；
P(X2＝8)＝0.3，
P(X2＝9)＝0.4，
P(X2＝10)＝0.1，
所以甲，乙各打一枪共击中18环的概率为：
P＝0.1×0.1＋0.3×0.4＋0.2×0.4＝0.21.
(2)甲的期望E(X1)＝5×0.1＋6×0.1＋7×0.1＋8×0.1＋9×0.2＋10×0.4＝8.4.
乙的期望E(X2)＝7×0.2＋8×0.3＋9×0.4＋10×0.1＝8.4.
甲的方差D(X1)＝(5－8.4)2×0.1＋(6－8.4)2×0.1＋(7－8.4)2×0.1＋(8－8.4)2×0.1＋(9－8.4)2×0.2＋(10－8.4)2×0.4＝3.04.
乙的方差为D(X2)＝(7－8.4)2×0.2＋(8－8.4)2×0.3＋(9－8.4)2×0.4＋(10－8.4)2×0.1＝0.84.
由于D(X1)＞D(X2)，故乙比甲技术稳定．