问题
解答题
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各件产品相互独立。
(Ⅰ)记x(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(Ⅱ)求生产4件甲产品所获得的利润不少于10万元的概率。
答案
解:(Ⅰ)由题设知,X的可能取值为10,5,2,-3
且P(X=10)=0.8×0.9=0.72
P(X=5)=0.2×0.9=0.18
P(X=2)=0.8×0.1=0.08
P(X=-3)=0.2×0.1=0.02
由此得X的分布列为:
 ;
;
(Ⅱ)设生产的4件甲产品中一等品有n件,则二等品有(4-n)件,
由题设知4n-(4-n)≥10,解得: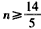
又n∈N,得n=3或n=4,
所以P= C43·0.83·0.2+C44·0.84=0.8192,
故所求概率为0.8192。
