问题
解答题
某地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18（假设两河流发生洪水与否互不影响）．现有一台大型设备正在该地工作，为了保护设备，施工部门提出以下三种方案：
方案1：运走设备，此时需花费4000元；
方案2：建一保护围墙，需花费1000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56 000元；
方案3：不采取措施，此时，当两河流都发生洪水时损失达60000元，只有一条河流发生洪水时，损失为10000元．
（1）试求方案3中损失费ξ（随机变量）的分布列；
（2）试比较哪一种方案好．
答案
（1）在方案3中，记“甲河流发生洪水”为事件A，“乙河流发生洪水”为事件B，
则P（A）=0.25，P（B）=0.18，
所以，有且只有一条河流发生洪水的概率为P（A?
+. B
?B）=P（A）?P（. A
）+P（. B
）?P（B）=0.34，. A
两河流同时发生洪水的概率为P（A?B）=0.045，
都不发生洪水的概率为P（
?. A
）=0.75×0.82=0.615，. B
设损失费为随机变量ξ，则ξ的分布列为：
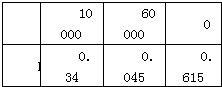
（2）对方案1来说，花费4000元；
对方案2来说，建围墙需花费1000元，它只能抵御一条河流的洪水，
但当两河流都发生洪水时，损失约56000元，而两河流同时发生洪水的概率为P=0.25×0.18=0.045．
所以，该方案中可能的花费为：1000+56000×0.045=3520（元）．
对于方案来说，损失费的数学期望为：Eξ=10000×0.34+60000×0.045=6100（元），
比较可知，方案2最好，方案1次之，方案3最差．