问题
计算题
如图所示，xOy平面内，第二象限匀强电场方向水平向右，第一象限匀强电场方向竖直向下，场强大小相等，设为E，而x轴下方区域有垂直于纸面向外的匀强磁场，磁感应强度设为B，图中OP直线与纵轴的夹角α=45°，一带正电的粒子从OP盲线上某点A（-L，L）处由静止释放，重力不计，设粒子质量为m，带电量为q，E、B、m、q均未知，但已知各量都使用国际制单位时，从数值上有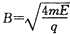
。
（1）求粒子进入磁场时与x轴交点处的横坐标；
（2）求粒子进入磁场时速度方向与x轴正方向的夹角；
（3）如果在OP直线上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。（提示：写出圆心点坐标x、y的函数关系）
答案
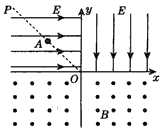
解：如图所示，带电粒子先做匀加速直线运动，进入第一象限后做类平抛运动，然后在磁场中做匀速圆周运动
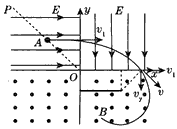
（1）设粒子进入第一象限的初速度为v1，根据动能定理有：
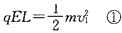
类平抛过程中：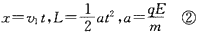
联立解得：x=2L
（2）类平抛过程的末速度设为v，竖直分速度为vy
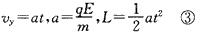
解得vy并与①式比较得：vy=v1
所以，v与x轴正方向的夹角为45°
（3）由前两问知：L取任意值时均有：x=2L，α=45° ④
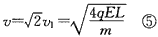
粒子在磁场中做匀速圆周运动时，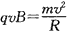
又由题意知，数值上有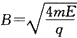
，联立各式求解R，解得从数值上有：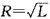
于是由图可知圆心点坐标：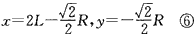
将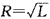
代入并消去变量L得：x=4y2+y，此为一抛物线方程，故各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线