问题
解答题
现有4个人去参加娱乐活动，该活动有甲、乙两个游戏可供参加者选择，为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏。
（1）求这4个人中恰有2人去参加甲游戏的概率；
（2）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；
（3）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ=|X-Y|，求随机变量ξ的分布列与数学期望Eξ。
答案
解：依题意，这4个人中，每个人去参加甲游戏的概率为
，去参加乙游戏的人数的概率为
设“这4个人中恰有2人去参加甲游戏”为事件Ai（i=0，1，2，3，4），
∴P（Ai）=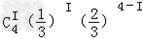
。
（1）这4个人中恰有2人去参加甲游戏的概率为P（A2）=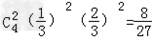
；
（2）设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B，则B=A3∪A4，
∴P（B）=P（A3）+P（A4）=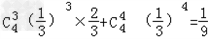
。
（3）ξ的所有可能取值为0，2，4，
由于A1与A3互斥，A0与A4互斥，
故P（ξ=0）=P（A2）=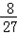
P（ξ=2）=P（A1）+P（A3）=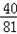
，
P（ξ=4）=P（A0）+P（A4）=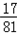
∴ξ的分布列是
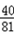
Eξ=0×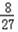
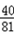+2×+4×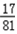
=
。