问题
解答题
已知方程x3-（1+2·3m）x2+（5n+2·3m）x-5n=0。
（1）若n=m=0，求方程的根；
（2）找出一组正整数n，m，使得方程的三个根均为整数；
（3）证明：只有一组正整数n，m，使得方程的三个根均为整数。
答案
解：（1）若n=m=0，则方程化为x3-3x2+3x-1=0，
即（x-1）3=0，
所以x1=x2=x3=1；
（2）方程化为（x-1）（x2-2·3mx+5n）=0，
设方程x2-2·3mx+5n=0的两个解为x1，x2
则x1，2=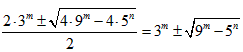
，
当m=n=1时，方程的三个根均为整数；
（3）设9m-5n=k2（其中k为整数）
所以9m-k2=5n，即（3m-k）（3m+k）=5n，
不妨设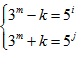
（其中i+j=n，i，j为非负整数），
因此：2·3m=5j（5j-i+1），
又∵5不能整除2·3m，
∴i=0，
因此有2·43m=5n+1，要使三根均为整数，则只有一组正整数m=n=1，
此时x1=x2=1，x3=5。