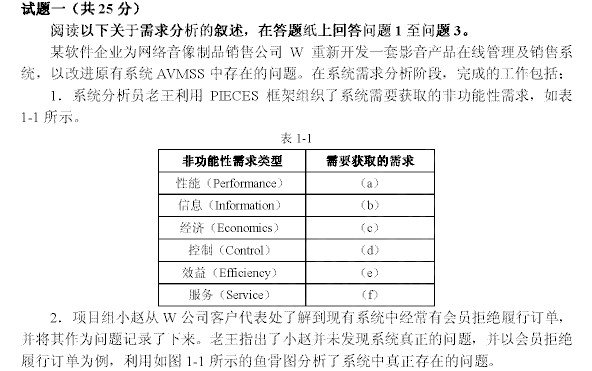
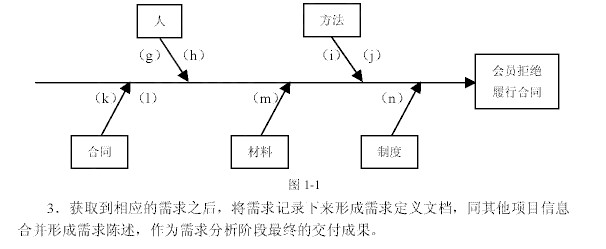
问题
解答题
设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=
|
答案
由勾股定理得,c2=a2+b2.
又∵c=
ab-(a+b),得c2=[1 3
ab-(a+b)]2=1 3
(ab)2-1 9
ab(a+b)+(a+b)2.2 3
即a2+b2=
(ab)2-1 9
ab(a+b)+a2+2ab+b2.2 3
整理得,ab-6(a+b)+18=0,即(a-6)(b-6)=18,
∵a,b均为正整数,不妨设a<b,
可得
或a-6=1 b-6=18
或a-6=2 b-6=9
,a-6=3 b-6=6
可解出
或a=7 b=24 c=25
或a=8 b=15 c=17
,a=9 b=12 c=15 .
∴满足条件的直角三角形有3个.
故答案为:3.